2021.12.27
データサイエンティスト、データアナリストになるには? はじめの一歩「統計検定4級」に受かる勉強法
はじめに
こんにちは!
メンバーズデータアドベンチャーカンパニー所属の石原寛太(いしはら かんた)と、メンバーズキャリアカンパニー所属の森 研人(もり けんと)です。
昨今、私達エンジニアを含む社会人には、世の中で活躍するためには何らかの実践的な付加価値が必要であると言われています。その付加価値のひとつに「データを見て分析・判断する」という能力があります。
この記事ではその指標を測る統計検定4級について書いていきます。
統計検定4級は、これからデータサイエンティスト、データアナリストを目指す方の取っ掛かりとも言えるので、少しでも参考になれば幸いです!
統計検定とは?
公式サイトにわかりやすく一言でまとめられています。
「統計検定」は、統計に関する知識や活用力を評価する全国統一試験です。
引用:統計検定、「統計検定とは」、https://www.toukei-kentei.jp/about/(2021年12月24日)
様々なことが書かれていますが、具体的に書き表すと、
「表やグラフを見て、要求(試験なら問題文)に合った計算ができ、その結果から何が言えるか、そこまで説明できるか(試験では正しい選択肢にチェックできるか)」
といった能力を、この検定では求められています。
ただしあくまで検定は指標であり、この資格を取ったからと言って「私は統計ができる!データを扱う案件は任せてください!」のような証明にはなりません。
資格を取るために身につけた知識や考え方を実務に活かす、実際に使われている分析方法を理解し自分のものにする。その力を試験勉強で得ることが遥かに大切である、ということを忘れてはいけません。
「統計検定4級」はどれ程の難易度?
公式サイトの文章を引用すると、
(1) 基本的な用語や概念の定義を問う問題(統計リテラシー)
(2) 用語の基礎的な解釈や2つ以上の用語や概念の関連性を問う問題(統計的推論)
(3) 具体的な文脈に基づいて統計の活用を問う問題(統計的思考)
引用:統計検定、「統計検定 4級」、https://www.toukei-kentei.jp/about/grade4/(2021年12月24日)
この3点を問われると表記されています。
もっと具体性を持った言い方に変えると、
(1) 統計リテラシー:~グラフ、~図、~表といった正しい見方はできるか?(例えば広告の『~第1位!〇か月で△%の効果が』といったデータはちゃんと解釈できているか)
(2) 統計的推論:例として「平均値・中央値・最頻値」が出され、これらの概要と関連性、グラフで表されたらこれを指している、といった理解はできているか?
(3) 統計的思考:文章や図を見て、どういったデータ(試験ならば問題文に基づいた回答)が求められているか理解できているか?
といったことを指しています。
パッと見は似たような言葉ですが、言語化するとニュアンスがそれぞれ異なり、どれもデータ分析・統計には必須のスキルです。
と書き表したものの、4級で扱う用語は一般的に使われている言葉もあり、考え方自体も方程式を使わずに解けるものが非常に多いです。
義務教育である中学数学を学んでいれば十分太刀打ちできます。必要以上に身構えず、タイトル通り統計の取っ掛かりである級であると気楽に受けていきましょう! (もちろん、だからと言ってノー勉は厳禁です!)
統計検定4級の内容を一部紹介
質的データと量的データの違いと、度数分布表について説明しようと思います(後述の勉強会で最も質問の多かったのがこの3つです)。
まず質的データとは、分類や種類を区別するためのデータであり、そのままでは足したり引いたり演算のできない変数のことを言います。例としては、「年齢、血液型、好きな食べ物」が含まれます。
そして、量的データとは、数値として意味のあるデータであり、演算ができる変数のことを言います。例としては、「人数、金額、身長」が含まれます。
しかし、この説明だけでは十分ではなかったため、データについてより細かく説明します。
質的データと量的データは、以下の画像のように名義尺度、順序尺度、間隔尺度、比率尺度の四つの項目に分類できます。
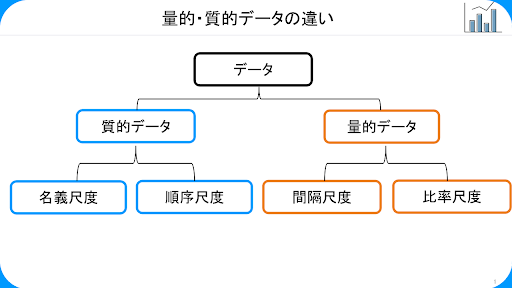
次に、それぞれの項目について説明していきます。
名義尺度
名義尺度とは、純粋な分類であり、順序に意味がない分類のことをいいます。
例えば、A型を1、B型を2、O型を3としたとき、A型が1でB型が2だから、数値の大きいB型のほうが優れているとはなりません。また、A型1+B型2=O型3 ともなりません。
アンケートや、集計を分析しやすくするために数字に置き換えているだけのものになります。
順序尺度
順序尺度とは、順序に意味がある分類のことをいいます。
例えば、アンケートの結果を(1.大変良い 2.良い 3.普通 4.悪い 5.とても悪い)としたとき、1に近づくにつれて「良い」ことを意味するため、順番に意味があると言えます。しかし、2.良い + 3.普通 =5.とても悪いとはなりません。すなわち計算することには意味のない数値です。
間隔尺度
間隔尺度は、数値の間隔(数値の差)に意味があることや、数値の大小に意味があることを特徴としています。また、0が何もないことを意味しません。
例)
50℃と40℃には温度差がある。
50℃のほうが高いことを意味する。
0℃は温度がないというわけではない。
比率尺度
比率尺度は、数値の間隔(数値の差)に意味があり、数値の大小に意味があることを特徴としています。また、0が何もないことを意味します。
例)
長さ30cmと20cmには長さの差がある。
30cmのほうが長いことを意味する。
0cmは長さがないということを表す。
ここまで、四つの項目について説明してきました。実際に理解できたかどうか確認するために例題を用意したので、ぜひ解いてみてください。
Q.次の項目は順序尺度、名義尺度、比率尺度、間隔尺度のいずれに該当するか。
1.電話番号 2.家賃 3.方角 4.震度 5.年齢
A.
1.電話番号→名義尺度。番号に数値的な意味はない。
2.家賃 →比率尺度。数値の大小に意味があり、0が何もないことを意味する
3.方角 →名義尺度。単純な分類。西より東のほうが優れていることはない。
4.震度 →順序尺度。震度6は震度3よりも揺れが大きいといえるが震度6が震度3の倍の揺れというわけではない。
5.年齢 →比率尺度。40歳は20歳の倍生きたといえる。
いかがでしょうか。全問正解できましたか?
度数分布表
度数分布表とは「データを任意の範囲ごとに分割し、それぞれの範囲内に存在するデータ数を表にまとめたもの」です。
以下のようなデータを考えてみましょう。
| 56 | 84 | 19 | 82 | 73 |
| 73 | 62 | 50 | 99 | 99 |
| 62 | 98 | 19 | 66 | 14 |
| 59 | 97 | 81 | 88 | 35 |
| 88 | 79 | 25 | 59 | 60 |
| 80 | 47 | 25 | 36 | 71 |
| 27 | 24 | 61 | 66 | 96 |
| 83 | 21 | 41 | 96 | 41 |
| 71 | 49 | 51 | 31 | 5 |
| 20 | 26 | 26 | 41 | 74 |
このままだとデータの羅列に過ぎないので、一目で特徴を把握することができません。
そこで、まずデータを降順に並べ替えてみます。
| 5 | 26 | 50 | 66 | 83 |
| 14 | 27 | 51 | 71 | 84 |
| 19 | 31 | 56 | 71 | 88 |
| 19 | 35 | 59 | 73 | 88 |
| 20 | 36 | 59 | 73 | 96 |
| 21 | 41 | 60 | 74 | 96 |
| 24 | 41 | 61 | 79 | 97 |
| 25 | 41 | 62 | 80 | 98 |
| 25 | 47 | 62 | 81 | 99 |
| 26 | 49 | 66 | 82 | 99 |
ここで、値が0~19のものを探すと、表のオレンジの部分だとわかります。データ数を数えてみると、4個のデータがあることもわかります。
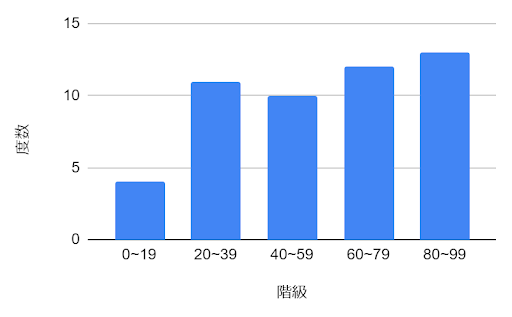
このようにほかの範囲の値もまとめていくと、下記のような度数分布表が完成します。
| 階級 | 度数 |
|---|---|
| 0~19 | 4 |
| 20~39 | 11 |
| 40~59 | 10 |
| 60~79 | 12 |
| 80~99 | 13 |
階級は「データを区切る範囲」、度数は「データの個数」を表します。
さらにここから度数分布表をより細かく作成するため一手間加えると、このような表になります。
| 階級 | 度数 | 累積度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 0~19 | 4 | 4 | 0.08 | 0.08 |
| 20~39 | 11 | 15 | 0.22 | 0.3 |
| 40~59 | 10 | 25 | 0.2 | 0.5 |
| 60~79 | 12 | 37 | 0.24 | 0.74 |
| 80~99 | 13 | 50 | 0.26 | 1 |
階級・・・・・・・データを区切る範囲
度数・・・・・・・区切られた範囲に存在する、データの個数
累積度数・・・・・その階級までのすべての度数の合計
相対度数・・・・・それぞれの階級の度数が全体占める割合
累積相対度数・・・その階級までのすべての相対度数の合計
これらを確認することで、データの羅列だけではいまいち掴み切れなかった、データの全体像や偏りが把握しやすくなります。
更に下図のヒストグラムように、グラフに書き換えられます。
更に更に、表や書き換えたグラフをもとに別のデータとの連携や比較ができるようになります。
資格勉強だけで終わらせず、「あ、このグラフは~だ!」「この値は~データだな」といった日常生活でも発見、考えられるようになりたいですね。
4級に向けた勉強方法、参考書・サイト(筆者目線)
まずは過去問!
前記した通り、4級自体は中学生まで身に着けた数学のノウハウで解けます。 そのため参考書やサイトを見てから~ではなく、4級に限っては過去問から取り組むのを勧めます。この時点で解けなくても気にしないでください。
過去問は公式サイトに一回分あります。(2021/12/24現在、2021年6月の問題が上がっています)
https://www.toukei-kentei.jp/about/grade4/#pastp
試験時間は60分で問題数は30問と、多くの方が問題数に対して時間が足りないと感じると思います。それを身をもって知るだけでも大きな収穫です。
数学が得意な方は「この過去問だけで十分」という人もいるかもしれません。
参考書で勉強
過去問をやって自分の足りなかった知識を得ましょう。
公式から過去問題集や参考書も出されていますし、検索すれば他出版社からの問題集もあります。
公式テキスト:http://www.tokyo-tosho.co.jp/books/978-4-489-02325-5/
公式過去問集:https://jitsumu.hondana.jp/book/b496705.html
筆者談ですがこの2冊でしっかりやり苦手意識をつぶしていけば、高得点者表彰も掴めると思います。
<h3勉強時間は心配ならば2週間は欲しい4級は決して難しくないとは書きましたが、過去問もやらずノー勉で挑んで合格できる……という資格ではありません。(できる方ももちろんいますが、それは学生時代に数学ができた方です)
数学や統計にあまり触れていない方なら、2週間は毎日参考書や過去問題集を進めることを推奨します。1日当たり1~2時間やれれば上出来だと思います。
ご参考ください!
おまけ:4級の勉強会を開きました!
メンバーズでは統計検定の取得が必須になりました。なんと2021年中に全員取得が掲げられています。
そのため私達は今回は講義式、試験範囲説明~演習問題を皆さんと解くまで、2回別々のカリキュラムでメンバーズ全社員に向け、オンラインで勉強会を開催しました。
この勉強会の参加者は計50人を超え、参加者からも「この勉強会のおかげで勉強が進んだ」「4級実際に取れました!」といった感想をいただきました。
勉強会を開催した身としましてはとても嬉しい言葉でした。
終わりに
ざっとではありますが、統計検定の説明から実例を出した解説の一部、勉強会の開催まで書き表しました。
再度記しますが統計検定は資格であり、決してこれを持っているからすごい・偉いというわけではありません。取得に向けて勉強して得た考え方がとても大切です。
この記事で少しでも統計に、データ分析に興味を持ってくだされば幸いです!
ありがとうございました!
この記事を書いた人

石原 寛太
メンバーズデータカンパニー所属の石原です。データ分析に悪戦苦闘の毎日です。。。趣味でバイク乗ってたりします。焼酎は芋しか勝たん。

森 研人
メンバーズキャリア所属。DXプロデューサーを目指し日々精進しています。主に本記事の勉強会の資料作成・運用・告知を行っていました。鹿せんべい飛ばし大会に参加したい今日この頃。



